Question

A thin rod (length = 2.97 m) is oriented vertically, with its bottom end attached to the floor by means of a frictionless hinge. The mass of the rod may be ignored, compared to the mass of the object fixed to the top of the rod. The rod, starting from rest, tips over and rotates downward. (a) What is the angular speed of the rod just before it strikes the floor? (Hint: Consider using the principle of conservation of mechanical energy.)(b) What is the magnitude of the angular acceleration of the rod just before it strikes the floor?

Answer 1

a) w = 2.57 rad / s , b) α = 3.3 rad / s²

Step-by-step explanation:

a) Let's use the conservation of mechanical energy, we will write it in two points the highest and when touching the ground

Initial. Higher

Em₀ = U = m g h

Final. Touching the ground

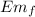`Em_(f)` = K = ½ I w²

How energy is conserved

Em₀ =
`Em_(f)`

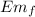
mg h = ½ I w2

The moment of specific object inertia

I = m L²

We replace

m g h = ½ (mL²) w²

w² = 2g h / L²

The height of the object is the length of the bar

h = L

w = √ 2g / L

w = √ (2 9.8 / 2.97)

w = 2.57 rad / s

b) the angular acceleration can be found from Newton's second rotational law

τ = I α

W L = I α

mg L = (m L²) α

α = g / L

α = 9.8 / 2.97

α = 3.3 rad / s²