Question

In 2013, the Pew Research Foundation reported that "45% of U.S. adults report that they live with one or more chronic conditions".^39 However, this value was based on a sample, so it may not be a perfect estimate for the population parameter of interest on its own. The study reported a standard error of about 1.2%, and a normal model may reasonably be used in this setting. Create a 95% confidence interval for the proportion of U.S. adults who live with one or more chronic conditions. Also interpret the confidence interval in the context of the study.

Answer 1

Answer with explanation:

Formula to find the confidence interval for population proportion (p) is given by :-

`\hat{p}\pm z^* SE`

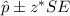
, where z* = Critical value.

`\hat{p}` = Sample proportion.

SE= Standard error.

Let p be the true population proportionof U.S. adults who live with one or more chronic conditions.

As per given , we have

`\hat{p}=0.45`

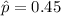
SE=0.012

By z-table , the critical value for 95% confidence interval : z* = 1.96

Now , a 95% confidence interval for the proportion of U.S. adults who live with one or more chronic conditions.:

`0.45\pm (1.96) (0.012)`

`0.45\pm (0.02352)`

`=(0.45-0.02352,\ 0.45+0.02352)=(0.42648,\ 0.47352)`

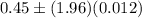
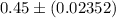
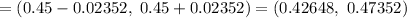
Hence, a 95% confidence interval for the proportion of U.S. adults who live with one or more chronic conditions.
`=(0.42648,\ 0.47352)`

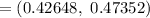
Interpretation : Pew Research Foundation can be 95% confident that the true population proportion (p) of U.S. adults who live with one or more chronic conditions lies between 0.42648 and 0.47352 .