Answer:
C)30%
Explanation:
Prime numbers less than 30 are given below
2,3,5,7,11,13,17,19,23,29
We have to find the probability that sum of three prime numbers selected will be even.
We know that
Sum of any three prime number except 2 will be odd.
Total prime numbers except 2=9
Total prime numbers=10
Probability:P(E)=
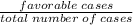
Probability of getting sum of three prime numbers selected will be odd=
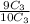
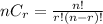
By using formula
Probability of getting sum of three prime numbers selected will be odd=P(E)=

Probability of getting sum of three prime numbers selected will be odd=P(E)=
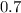
Probability of getting sum of three prime numbers selected will be even=P(E')=1-0.7=0.3=
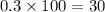 %
%
By using formula P(E')=1-P(E)