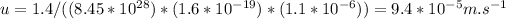Question

Calculate the average drift speed vd of electrons traveling through a copper wire with a cross-sectional area of 1.10 mm2 when carrying a current of 1.40 A (values similar to those for the electric wire to your study lamp). It is known that about one electron per atom of copper contributes to the current. The atomic weight of copper is 63.54 grams/mol, and its density is 8.92 g/cm3. First, calculate the number of current carrying electrons per unit volume, n.

n=
Drift Speed vd= m/s

Answer 1

The answer is
`9.4*10^(-5) ms^(-1)`

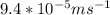
Step-by-step explanation:

The equation of the drift velocity is given by,

`u = I/nAq`

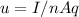
where I is the current which is given in the question as 1.4 Amp. q is the charge on the electron which we know for a fact to be
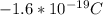`-1.6*10^(-19) C`. A is the cross sectional area of the conductor which we are also given but in mm2. So we will first have to convert this to m2 which is through very basic conversion technique equal to
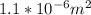`1.1*10^(-6) m^(2)` . We only need to determine the n which is equal to number of electron per unit volume. From the question we can see that the number of moles available in unit
`cm^(3)` is
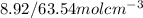`8.92/63.54 mol cm^(-3)` . This number in m3 instead of cm3 using basic unit conversion would be equal to
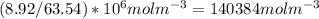`(8.92/63.54)*10^(6)molm^(-3) = 140384 molm^(-3)` . You take this number and multiply it by the avagardo number which tells you how many number of atoms are present in a mole which is equal to
`6.02*10^(23)` which gives us the number of atoms per unit m3 . Which will also be equal to number of electrons per unit m3 since each atom contributes 1 electron to the electric current. So n is equal to ,

`n = 140384 * 6.02*10^(23) = 8.45*10^(28) electrons.m^(-3)` .

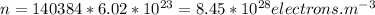So now we have all 4 quantities required for the calculation of the drift velocity. We get our answer by plugging the values in the drift velocity equation,

`u = 1.4/((8.45*10^(28))*(1.6*10^(-19))*(1.1*10^(-6))) = 9.4*10^(-5)m.s^(-1)`