Answer:
a.
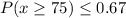
b.P(40<x<60)
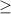 0.75
0.75
Explanation:
We are given that
Mean =E(X)=50
a.We have to find the probability when x greater than or equal to 75.
Markovs inequality
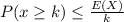
By using Markovs inequality and substitute k=75
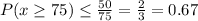
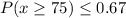
b.We have to find P(40<x<60)
Variance=
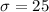
Chebyshev's inequality:
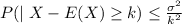
Because 50+10=60 and 50-10=40
Therefore, k=10
By using Chebyshev's inequality and substitute k=10
because 50+10=60 and 50-10=40
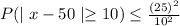
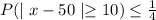
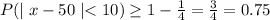
Hence, P(40<x<60)
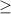 0.75
0.75