Question

A man stands on a platform that is rotating (without friction) with an angular speed of 1.2 rev/s; his arms are outstretched and he holds a brick in each hand.

The rotational inertia of the system consisting of the man, bricks, and platform about the central vertical axis of the platform is 6.0 kg·m2.

If by moving the bricks the man decreases the rotational inertia of the system to 2.0 kg·m2, what are

(a) the resulting angular speed of the platform and

(b) the ratio of the new kinetic energy of the system to the original kinetic energy?

(c) What source provided the added kinetic energy?

Answer 1

a) w₂ = 22.6 rad / s , b)
`K_(f)` / K₀ = 3

Step-by-step explanation:

a) This exercise we must define the system as formed by the platform, the man and bricks, for this system as a whole the forces are internal the angular momentum is conserved, let's write in two instants

Initial. Greater moment of inertia

L₀ = I₁ w₁

Final. Less moment of inertia

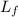`L_(f)` = I₂ w₂

L₀ =
`L_(f)`

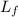
I₁ w₁ = I₂ w₂

w₂ = I₁ / I₂ w₁

We reduce to the SI system

w₁ = 1.2 rev / s (2π rad / 1 rev) = 7.54 rad / s

w₂ = 6.0 / 2.0 7.54

w₂ = 22.6 rad / s

b) Let's look for kinetic energy in both moments

Initial

K₀ = ½ I₁ w₁²

K₀ = ½ 6.0 7.54²

K₀ = 170.55 J

Final

`K_(f)` = ½ I₂ w₂²

`K_(f)` = ½ 2.0 22.6²

`K_(f)` = 510.76 J

We look for the relationship

`K_(f)` / K₀ = 510.76 / 170.55

`K_(f)` / K₀ = 3

c) The change in angular momentum is what creates the change in kinetic energy, of course the total mechanical energy is conserved as the potential energy decreases