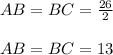Answer:
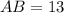
Explanation:
The missing figure is attached.
For this exercise it is important to remember the definition of a "Median of a triangle".
A median of a triangle is defined as a line segment that joins a vertex of the triangle to the midpoint of the opposite side. Then, there are three medians in a triangle.
The point in which all the medians intersect is called "Centroid".
In this case know that "DB" is a median of the triangle ACD. Then, it divides the lenght "AC" into two equal parts. This means that:
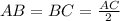
According to the data given in the exercise, you know that:
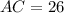
Then, subsitituting this value into the equation wrote above, you get that: