Question

A merry-go-round is rotating at an angular speed of 0.2 radians/s. Its motor falls off and it rotates freely. A technician jumps on the edge along the direction of the radius. The angular velocity after he lands is 0.04 radians/s. The moment of inertia of the technician, in (kg m2 ) with respect to the axis of the merry-go-round’s axis of rotation is 5000 kg m2 . What is the moment of inertia of the merry-go-round?

Answer 1

I₁ =1250 kg.m²

Step-by-step explanation:

Given that

Angular speed of Merry ,ω₁= 0.2 rad/s

Angular speed of technician ,ω₂= 0.04 rad/s

Moment of the inertia of the technician ,I₂= 5000 kg.m²

Lets assume that

Moment of the inertia of merry with respected to the ground=I₁

There is no any external torque ,that is why angular momentum of the system will be conserve.

Now by conserving angular momentum

I₁ ω₁=(I₁+I₂)ω₂

I₁ x 0.2 = (I₁ +5000 ) x 0.04

I₁ (0.2-0.04) = 5000 x 0.04

`I_1=(5000* 0.04)/(0.2-0.04)`

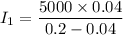
I₁ =1250 kg.m²