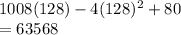Answer:
63568 dollars
Explanation:
Given that in your computer store you charge $1012 per computer sold. Your costs are given by the equation
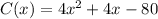
where x is the number of computers sold.
Revenue = sales price *no of computers sold
= 1012x
Profit = Revenue - cost
=
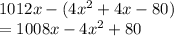
Use derivative test to find maximum profit

Equate I derivative to 0
x= 128
i.e. if 128 computers are manufactured and sold profit wouldbemaximum
Profit maximum=