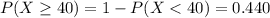Question

Suppose that when a transistor of a certain type is subjected to an accelerated life test, the lifetime x (in weeks) has a gamma distribution with mean 40 weeks and variance 320 weeks.

A) What is the probability that a transistor will last between 1 and 40 weeks?

B) What is the probability that a transistor will last at most 40 weeks?

Answer 1

a)
`P(1 \leq X \leq 40)`

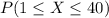
In order to find this probability we can use excel with the following code:

=GAMMA.DIST(40;5,8,TRUE)-GAMMA.DIST(1,5,8,TRUE)

And we got:

`P(1 \leq X \leq 40)=0.560`

b)
`P(X \geq 40)=1-P(X<40)`

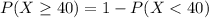
In order to find this probability we can use excel with the following code:

=1-GAMMA.DIST(40,5,8,TRUE)

And we got:

`P(X \geq 40)=1-P(X<40)=0.440`

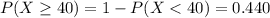
Explanation:

Previous concepts

The Gamma distribution "is a continuous, positive-only, unimodal distribution that encodes the time required for
`\alpha` events to occur in a Poisson process with mean arrival time of
`\beta`"

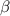Solution to the problem

Let X the random variable that represent the lifetime for transistors

For this case we have the mean and the variance given. And we have defined the mean and variance like this:

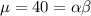`\mu = 40 = \alpha \beta` (1)

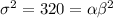`\sigma^2 =320= \alpha \beta^2` (2)

From this we can solve
`\alpha` and [/tex]\beta[/tex]

From the condition (1) we can solve for
`\alpha` and we got:

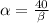`\alpha= (40)/(\beta)` (3)

And if we replace condition (3) into (2) we got:

`320= (40)/(\beta) \beta^2 = 40 \beta`

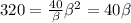
And solving for
`\beta = 8`

And now we can use condition (3) to find
`\alpha`

`\alpha=(40)/(8)=5`

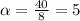
So then we have the parameters for the Gamma distribution. On this case
`X \sim Gamma (\alpha= 5, \beta=8)`

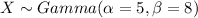
Part a

For this case we want this probability:

`P(1 \leq X \leq 40)`

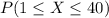
In order to find this probability we can use excel with the following code:

=GAMMA.DIST(40;5,8,TRUE)-GAMMA.DIST(1,5,8,TRUE)

And we got:

`P(1 \leq X \leq 40)=0.560`

Part b

For this case we want this probability:

`P(X \geq 40)=1-P(X<40)`

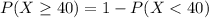
In order to find this probability we can use excel with the following code:

=1-GAMMA.DIST(40,5,8,TRUE)

And we got:

`P(X \geq 40)=1-P(X<40)=0.440`