Answer:
z=i+2
,
z=i-2
Explanation:
Remember that the quadratic equation
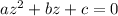 has the complex solutions
has the complex solutions
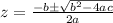 (this is the quadratic formula).
(this is the quadratic formula).
Apply this with a=1, b=-2i and c=-5 to get:
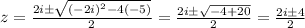 . Then the solutions are
. Then the solutions are
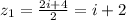 and
and
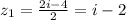
It isn't necessary to use De Moivre's formula.