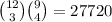Question

A class of twelve computer science students are to be divided into three groups of 3, 4, and 5 students to work on a project. How many ways can this be done if every student is to be in exactly one group

Answer 1

27720

Explanation:

Denote by
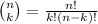`\binom{n}{k}=(n!)/(k!(n-k)!)` the binomial coefficient "n choose k". Given k<n,
`\binom{n}{k}` is the number of ways of choosing k elements from a set of n elements (the order in which we choose the elements doesn't matter).

First, we can form the group of 3 students. This is done by choosing 3 students from the class of 12 students, so it can be done in
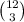`\binom{12}{3}` ways. We can't repeat students, then we must form the other groups from the remaining 9 students. If we next form the group of 4 students, there are
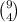`\binom{9}{4}` ways of choosing it. Now, there remain 5 students without a group, so they have to conform the group of 5 and this can only be done in 1 way. By the multiplication principle, the number of ways of forming the groups is
`\binom{12}{3}\binom{9}{4}=27720`