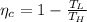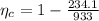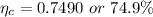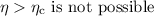Answer:
a)
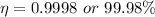
b)
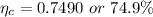
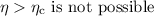
Step-by-step explanation:
Given:
- temperature of source reservoir,

- temperature of sink reservoir,
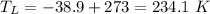
- quantity of aluminium frozen by the engine during 1 cycle,

- quantity of mercury melted by the engine during 1 cycle,
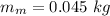
- latent heat of fusion of aluminium,
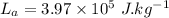
- latent heat of fusion of mercury,

a)
Heat absorbed by the engine:


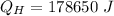
Heat rejected by the engine:

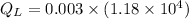
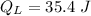
Now the efficiency of the engine:


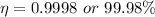
b)
Now the Carnot efficiency of the engine: