1 Answer

Manishh · Answer 1 · 2020-10-23T01:24:05+0000

Answer:

There is a 50% probability that the household has a dog, given that the household has a cat.

Explanation:

We solve this problem building the Venn's diagram of these probabilities.

I am going to say that:

A is the probability that a household has a cat.

B is the probability that a household has a dog.

We have that:

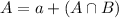
$A = a + (A \cap B)$

In which a is the probability that a household has a cat but not a dog and
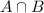$A \cap B$ is the probability that a household has both a cat and a dog.

By the same logic, we have that:

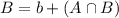
$B = b + (A \cap B)$

The probability that the household has a cat or a dog is 0.5

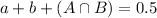
$a + b + (A \cap B) = 0.5$

The probability that the household has a dog is 0.4

B = 0.4

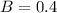
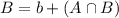
$B = b + (A \cap B)$

$b = 0.4 - (A \cap B)$

The probability that the household has a cat is 0.2.

A = 0.2

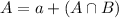
$A = a + (A \cap B)$

$a = 0.2 - (A \cap B)$

So

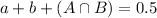
$a + b + (A \cap B) = 0.5$

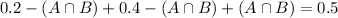
$0.2 - (A \cap B) + 0.4 - (A \cap B) + (A \cap B) = 0.5$

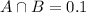
$A \cap B = 0.1$

What is the probability that the household has a dog, given that the household has a cat?

20% of the households have a cat, and 10% have both a cat and a dog. So

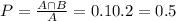
$P = (A \cap B)/(A) = {0.1}{0.2} = 0.5$

There is a 50% probability that the household has a dog, given that the household has a cat.

Please log in or register to add a comment.