Question

A motorcyclist is traveling along a road and accelerates for 4.84 s to pass another cyclist. The angular acceleration of each wheel is 6.76 rad/s2, and, just after passing, the angular velocity of each is 77.6 rad/s, where the plus signs indicate counterclockwise directions. What is the angular displacement of each wheel during this time?

Answer 1

296 rad

Step-by-step explanation:

time (t) = 4.84 s

angular acceleration (a) = 6.76 rad/s^{2}

angular velocity (ω) = 77.6 rad/s

what is the angular displacement (θ) of the wheel during this time?

from the equation of angular kinematics angular displacement (θ) = ω₀t +
`(1)/(2)at^(2)`

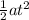
where

• a is angular acceleration = 6.76

• t is time = 4.84

• ω₀ is initial angular acceleration and can be gotten from the formula below

ω = ω₀ + at

77.6 = ω₀ + (6.76 x 4.84)

ω₀ = 77.6 - (6.76 x 4.84) = 44.88 rad/s

• now we can substitute all required values into the formula for angular displacement

angular displacement (θ) =ω₀t +
`(1)/(2)at^(2)`

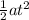
angular displacement (θ) =
`(44.88 x 4.84) + (1)/(2) x 6.76 x 4.84^(2)`

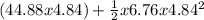
angular displacement (θ) = 296 rad