Question

The Sun orbits the center of the Milky Way galaxy once each 2.60 x 108 years, with a roughly circular orbit averaging 3.00 x 104 light years in radius. (A light year is the distance traveled by light in 1 y) Part (a) Calculate the centripetal acceleration of the Sun in its galactic orbit in m/s2 NumericA numeric value is expected and not an expression. Part (b) Calculate the average speed of the Sun in its galactic orbit in m/s. Numeric :A numeric value is expected and not an expression.

Answer 1

`1.66553* 10^(-10)\ m/s^2`

217494.87601 m/s

Step-by-step explanation:

Distance of Sun from the center of the Milky Way

`r=3* 10^8* 3* 10^4* 365.25* 24* 3600`

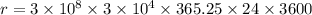
Angular speed is given by

`\omega=(2\pi)/(T)\\\Rightarrow \omega=(2\pi)/(2.6* 10^8* 365.25* 24* 3600)`

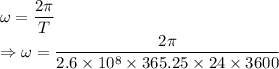
Centripetal acceleration is given by

`a_c=\omega^2r\\\Rightarrow a_c=\left((2\pi )/(2.6* \:10^8* 365.25* 24* 3600)\right)^2* 3* 10^8* 3* 10^4* 365.25* 24* 3600\\\Rightarrow a_c=1.66553* 10^(-10)\ m/s^2`

The centripetal acceleration is
`1.66553* 10^(-10)\ m/s^2`

Velocity is given by

`v=\omega r\\\Rightarrow v=(2\pi)/(2.6* 10^8* 365.25* 24* 3600)* 3* 10^8* 3* 10^4* 365.25* 24* 3600\\\Rightarrow v=217494.87601\ m/s`

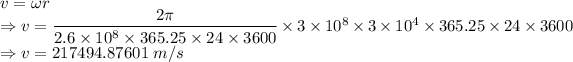
The average speed of the Sun in its galactic orbit is 217494.87601 m/s