Question

A volcano erupts and launches a chunk of hot magma horizontally with a speed of 252\,\dfrac{\text m}{\text s}252 s m ​ 252, start fraction, start text, m, end text, divided by, start text, s, end text, end fraction. The magma travels a horizontal distance of 1250\,\text m1250m1250, start text, m, end text before it hits the ground. We can ignore air resistance.

Answer 1

911m

Step-by-step explanation:

Answer 2

The final vertical velocity is -48.66 m/s,

Step-by-step explanation:

The full question is:

"A volcano erupts and launches a chunk of hot magma horizontally with a speed of 252 m/s The magma travels a horizontal distance of 1250 m before it hits the ground. We can ignore air resistance.

What is the vertical velocity of the magma when it hits the ground? "

In order to find the final vertical velocity, we can find first the time it takes to reach the ground, thus if we ignore air resistance horizontally we have uniform motion.

Time it takes to hits the ground.

For uniform motion we have the following equation

`x= x_0 +v_x t`

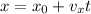
We can assume the initial position where the volcano is as
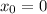`x_0=0`, so at x = 1250 we have:

`1250 \,m=0+252 \cfrac ms (t)`

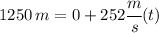
Thus we can solve for t by dividing both sides by 252 m/s to get

`t=4.96 \,s`

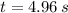
Final vertical velocity.

With the time we can work with the vertical velocity using free fall motion

`v_f_y=v_o_y-gt`

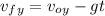
Since the chunk of magma was thrown horizontally the initial vertical velocity is 0,
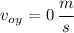`v_o_y=0 \, \cfrac ms`, so we get

`v_f_y =-gt \\ \\v_f_y= -9.81 \cfrac m{s^2} * 4.96 \,s`

Thus we get

`\boxed{v_f_y= -48.66 \cfrac ms}`

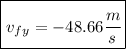
Thus the final vertical velocity is -48.66 m/s, the negative sign tell us that it is aiming down.