Question

Iodine-131, t1/2 = 8.0 days, is used in diagnosis and treatment of thyroid gland diseases. If a laboratory sample of iodine-131 initially emits 9.95 × 1018 β particles per day, how long will it take for the activity to drop to 6.22 × 1017 β particles per day?

Answer 1

Step-by-step explanation:

Formula for the first order decay is as follows.

`ln((A)/(A_(o)))` = -kt

where, A = activity at time t

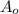`A_(o)` = initial activity

k = decay constant

Hence, putting the given values into the above formula as follows.

k =
`\frac{ln(2)}{\text{half life}}`

=
`(ln(2))/(8.0)`

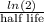
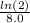
= 0.086643 per day

Also,
`(ln(6.22 * 10^(17)))/(9.95 * 10^(8)) = -0.086643 * t`

t = 32 days

Thus, we can conclude that it will take 32 days for the activity to drop to
`6.22 * 10^(17)`
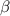`\beta` particles per day.