Step-by-step explanation:
The given data is as follows.
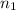 = 9,
= 9,
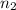 = ?
= ?
Z for hydrogen = 1
As we know that,
Energy (E) =

where, h = planck's constant =
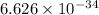 Js
Js
c = speed of light =
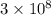 m/s
m/s
 = wavelength
= wavelength
According to Reydberg's equation, we will calculate the energy emitted by the photon as follows.
![\Delta E = -2.179 * 10^(-18) J * (Z)^(2)[(1)/(n^(2)_(2)) - (1)/(n^(2)_(1))]](https://img.qammunity.org/2020/formulas/chemistry/middle-school/9d3jjypt053dg3r1s86bzpi1g5ymsveys6.png)
or,
 =
=
![-2.179 * 10^(-18) J * (Z)^(2)[(1)/(n^(2)_(2)) - (1)/(n^(2)_(1))]](https://img.qammunity.org/2020/formulas/chemistry/middle-school/dj9vsy7o0rt7h2367nzdnz1tuvs3tcdunz.png)
Putting the given values into the above equation as follows.
 =
=
![-2.179 * 10^(-18) J * (Z)^(2)[(1)/(n^(2)_(2)) - (1)/(n^(2)_(1))]](https://img.qammunity.org/2020/formulas/chemistry/middle-school/dj9vsy7o0rt7h2367nzdnz1tuvs3tcdunz.png)
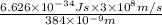 =
=
![-2.179 * 10^(-18) J * (1)^(2)[(1)/(n^(2)_(2)) - (1)/((9)^(2))]](https://img.qammunity.org/2020/formulas/chemistry/middle-school/qr8mhnzu8q3wg5ur04om9okzwk4ubqztpw.png)
n = 2
Thus, we can conclude that the final level of the electron is 2.