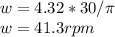Question

A 210 g , 32.0-cm-diameter turntable rotates on frictionless bearings at 56.0 rpm . A 18.0 g block sits at the center of the turntable. A compressed spring shoots the block radically outward along a frictionless groove in the surface of the turntable.

Answer 1

The question is not complete, below is the complete question

"A 210g, 32.0-cm-diameter turntable rotates on frictionless bearings at 56.0rpm. A 18.0g block sits at the center of the turntable. A compressed spring shoots the block radically outward along a frictionless groove in the surface of the turntable.

What is the turntable's rotation angular velocity when the block reaches the outer edge?"

answer = 41.3rpm

Step-by-step explanation:

First, we know that the angular momentum will change in value when the block sits on the turn table,but the net angular momentum before ad after will remain the same.

The angular momentum(L) is the rotational equivalent of the linear momentum express as

`L=Iw`

where I is the inertia and w is the angular speed.

Now let solve for the angular momentum at the initial stage

`L_(i)=Iw_(i)\\`.

where
`I=Mr^(2)`

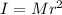
Hence we have

`L_(i)=(1)/(2)Mr^(2)w_(i) \\`

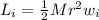
but r=diameter/2= 32/2=16cm=0.16m

mass,m=210g/1000=0.21kg

angular speed,w=56rpm we convert to rad/s by multiplying 56 by
`(\pi )/(2)`

W=
`56*(\pi )/(2) \\w=5.86rad/s\\`

By substituting values into the formula for the angular momentum we arrive at

`L_(i)=(1)/(2)*0.21* 0.16^(2) *5.86\\L_(i)=0.0315\\`

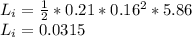
At the edge, we also compute the angular momentum

`L_(f)=(1)/(2)Mr^(2)w_(i) +mr^(2)w\\`

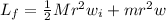
where m is the mass of the block= 18g=0.018kg.

if we substitute value

`L_(f)=(1)/(2)*0.21*0.16^(2)w+0.18*0.16^(2)w\\L_(f)=0.002688w+0.004608\\L_(f)=0.007296w`

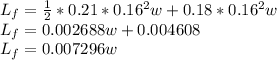
since angular momentum is conserved,

`L_(i)=L_(f)`

`0.0315=0.007296w\\w=(0.0315)/(0.007296) \\w=4.32rad/s\\`

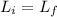
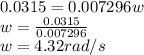
converting back to rpm

`w=4.32*30/\pi\\w=41.3rpm`