Answer: A. 85.7
Explanation:
Given : Two sections of a class took the same quiz.
Section A had 15 students who had a mean score of 80, and Section B had 20 students who had a mean score of 90.
We know that ,

Then , for section A :
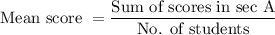

Similarly in Section B,
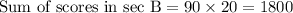
Total scores = Sum of scores in sec A+Sum of scores in sec B
=1200+1800=3000
Total students = Students in sec A +Students in sec B
=15+20=35
Now , the mean score for all of the students on the quiz =
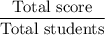
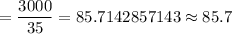
Hence, the approximate mean score for all of the students on the quiz = 85.7
Thus , the correct answer is option A. 85.7.