Question

Two functions are represented below. Which function has a domain that contains the domain of the other as a

subset?
f(x)=-log( X+3 ) - 2

Function g(x) f(x)

Subset g(x) f(x)

Answer 1

g has a domain that contains the domain of f as a subset

Explanation:

The Domain of Real Functions

Real functions take values for the independent variable (usually x). The whole set of those values is called the domain of f.

Function f is defined as

`f(x)=-log(x+3)-2`

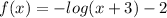
It can only exist when the argument is positive, i.e.

`x+3>0`

`x>-3, (-3,\infty)`

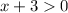
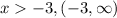
Function g is not explicitly defined but we can see its graph. It's evident its domain is

`(-5,\infty)`

This interval contains the domain obtained for f, so we can conclude g has a domain that contains the domain of f as a subset