Answer:
Launch speed is equal to
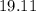 meter/second
meter/second
Step-by-step explanation:
Using the newton's equation, we know that
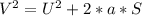
Where V is the final speed , U is the initial speed, a is the acceleration and S is the distance
At the highest point of the trajectory the object;s speed reduces to zero. hence
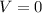
While initial velocity is equal to
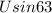 °
°

Substituting the given values we get -

Thus, launch speed is equal to
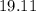 meter/second
meter/second