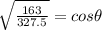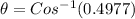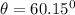Answer:
1.
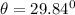
2.
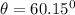
Step-by-step explanation:
Polarizes axis can create two possible angles with the vertical.
first we have to find the intensity of first polarizer
which is given as
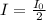
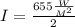
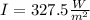
For a smaller angle for the first polarizer:
According to Malus Law
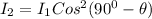
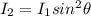
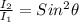
taking square root on both sides
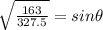
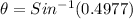
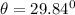
For a larger angle for the first polarizer:
According to Malus Law
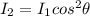
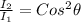
taking square root on both sides