Question

Use the matrix capabilities of a graphing utility to write the augmented matrix corresponding to the system of equations in reduced row-echelon form. Then solve the system. (If there is no solution, enter NO SOLUTION. If the system is dependent, express x, y, z, and w in terms of the parameter

a.) x + 2y + z + 3w = 0 x − y + w = 0 y − z + 2w = 0 (x, y, z, w) =

Answer 1

x =-2t , y = -t, z= t

Explanation:

x+2y+z+3w=0

x-y+w=0

y-z+2w=0

The augmented system would be given by:

`\begin{matrix}1 & 2 & 1 & 3 & 0\\1 & -1 & 0 & 1 & 0\\0 & 1 & -1 & 2 & 0\\\end{matrix}`

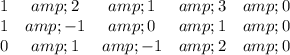
Now we can do operations in order to reduce it to the row echelon form

1) R1 *(-1) + R2

`\begin{pmatrix}1 & 2 & 1 & 3 & 0\\0 & -3 & -1 & -2 & 0\\0 & 1 & -1 & 2 & 0\\\end{pmatrix}`

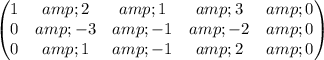
2) R2 *(-1/3)

`\begin{pmatrix}1 & 2 & 1 & 3 & 0\\0 & 1 & 1/3 & 2/3 & 0\\0 & 1 & -1 & 2 & 0\\\end{pmatrix}`

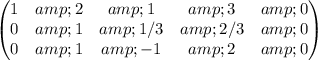
3) R2*(-1)+R3

`\begin{pmatrix}1 & 2 & 1 & 3 & 0\\0 & 1 & 1/3 & 2/3 & 0\\0 & 0 & -4/3 & 4/3 & 0\\\end{pmatrix}`

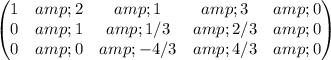
4) R3*(-3/4)

`\begin{pmatrix}1 & 2 & 1 & 3 & 0\\0 & 1 & 1/3 & 2/3 & 0\\0 & 0 & 1 & -1 & 0\\\end{pmatrix}`

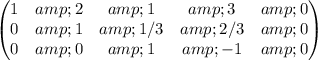
5) R3(-1/3) + R2; R3(-1) +R1

`\begin{pmatrix}1 & 2 & 0 & 4 & 0\\0 & 1 & 0 & 1 & 0\\0 & 0 & 1 & -1 & 0\\\end{pmatrix}`

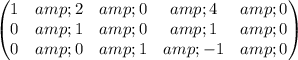
6) R2(-2) +R1

`\begin{pmatrix}1 & 0 & 0 & 2 & 0\\0 & 1 & 0 & 1 & 0\\0 & 0 & 1 & -1 & 0\\\end{pmatrix}`

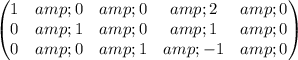
Let w=t a free variable then the solution is given by:

x =-2t , y = -t, z= t