Question

The rotating arm starts from rest and acquires a rotational speed N = 600 rev/min in 2 seconds with constant angular acceleration. Find the time t after starting before the acceleration vector of end P makes an angle of 45 with the arm OP

Answer 1

The time after starting is 0.178 sec.

Step-by-step explanation:

Given that,

Rotational speed = 600 rev/min

Time t = 2 sec

Angle = 45

Distance OP= 6''

According to figure,

We need to calculate the angular acceleration

Using formula of angular acceleration

`\alpha=(\omega)/(t)`

`\alpha=((2\piN)/(60))/(t)`

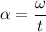
Put the value into the formula

`\alpha=((2*\pi*600)/(60))/(2)`

`\alpha=10\pi\ rad/s62`

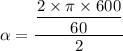
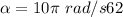
We need to calculate the tangential acceleration

Using formula of tangential acceleration

`a_(t)=OP* \alpha`

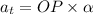
Put the value into the formula

`a_(t)=6*10\pi`

`a_(t)=60\pi\ in/s^2`

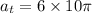
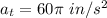
We need to calculate the normal acceleration

Using formula of normal acceleration

`a_(n)=OP*\omega^2`

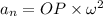
For angle
`\theta=45`

`a_(n)=a_(t)`

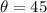
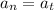
Put the value into the formula

`OP*\omega^2=60\pi`

`6*\omega^2=60\pi`

`\omega^2=10\pi`

`\omega=√(10\pi)`

`\omega=5.605\ rad/s`

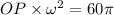
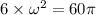
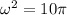
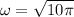
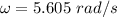
We need to calculate the time

Using the kinematics equation

`\omega=\omega_(0)+\alpha t`

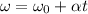
Put the value into the formula

`5.605=0+10\pi t`

`t=(5.605)/(10\pi)`

`t=0.178\ sec`

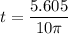
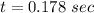
Hence, The time after starting is 0.178 sec.