Question

There are 50,000 households in a certain city. The average number of persons aged 16 and over living in each household is known to be 2.38, the SD is 1.87. A survey organization plans to take a simple random sample of 400 households and interview all persons age 16 and over living in the sample households. The total number of interviews will be around___give or take___or so.

Answer 1

The total number of interviews will be about 9552, give or take 37.4 or so.

Explanation:

Data given

Total of 50000 households

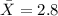`\bar X = 2.8` represent the average number of people in household

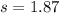`s= 1.87` represent the sample standard deviation of the number of people in household

n= 400 represent the sample size.

Solution to the problem

We can assume that the sample of 400 households are selected using random sampling from a grand box of 50000, and we select 400.

The expected value for the average number of people in a household is 2.38 and the standard deviation is 1.87.

We ar einterested on this case on the expected value for the sum and is defined as:

Expected value sum = Number selected * Expected value= 400*2.38=952

The reason of this is this one: From the definition of sample mean we have:

`\bar X =(\sum_(i=1)^n X_i)/(n) =(T)/(n)`

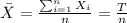
Where T represent the sum or the total, if we solve for T we got:

`T = n \bar x`

Assuming that
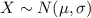`X\sim N(\mu, \sigma)` and if we find the expected value for the total and the variance we got:

`E(T) = n E (\bar X) = n \mu`

`Var(T) = n^2 Var(T) = n^2 \sigma^2`

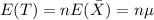
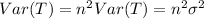
And the deviation would be:

`Sd(X) = \sqrt{n^2 (\sigma^2)/(n)}= √(n) \sigma`

And now the standard error for the sum is defined as the product of the square root of n and the single deviation of a box like this:

`SE = √(n) s= √(400) 1.87 =37.4`

So then the correct answer would be:

The total number of interviews will be about 9552, give or take 37.4 or so.