Question

Annual high temperatures in a certain location have been tracked for several years. Let XX represent the year and YY the high temperature. Based on the data shown below, calculate the correlation coefficient (to three decimal places) between XX and YY. Use your calculator!x y4 43.655 40.746 38.537 37.228 33.019 30.610 29.8911 27.1812 25.8713 23.5614 22.2515 18.6416 18.3317 16.9218 13.8119 9.9

Answer 1

r =-0.996

Explanation:

The correlation coefficient is a "statistical measure that calculates the strength of the relationship between the relative movements of two variables". It's denoted by r and its always between -1 and 1.

In order to calculate the correlation coefficient we can begin doing the following table:

n x y xy x*x y*y

1 4 43.65 174.6 16 1905.323

2 5 40.74 203.7 25 1659.748

3 6 38.53 231.18 36 1484.561

4 7 37.22 260.54 49 1385.323

5 8 33.01 264.08 64 1089.660

6 9 30.61 275.49 81 936.972

7 10 29.89 298.9 100 893.412

8 11 27.18 298.98 121 738.752

9 12 25.87 310.44 144 669.257

10 13 23.56 306.28 169 555.0974

11 14 22.25 311.50 196 495.063

12 15 18.64 279.60 225 347.450

13 16 18.33 293.28 256 335.989

14 17 16.92 287.64 289 286.286

15 18 13.81 248.58 324 190.716

16 19 9.9 188.10 361 98.01

`n =16 \sum x \sum y \sum xy \sum x^2 \sum y^2`

n=16
`\sum x = 184, \sum y = 430.11, \sum xy=4232.89, \sum x^2 =2456, \sum y^2 =13071.6`

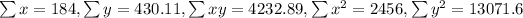
And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

`r=(16(4232.89)-(184)(430.11))/(√([16(2456) -(184)^2][16(13071.600) -(430.11)^2]))=-0.996`

So then the correlation coefficient would be r =-0.996