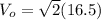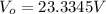To solve this problem it is necessary to apply the concepts related to Ohm's Law to find the voltage in the case of direct current. While for the Alternate current we use the concept of RMS voltage.
PART A) In the case of DC we have to,
V=IR
Where,
I = Current
R = Resistance
Where the current is 60mA y the resistance is
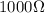 , then the potential would be
, then the potential would be
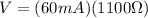
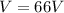
In the case of DC we have that the current and the RMS voltage is,
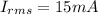
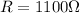

The potential in AC then is,