Question

The perimeter of a particular square and the circumference of a particular circle are equal. What is the ratio of the area of the square to the area of the circle? Express your answer as a common fraction in terms of $\pi$.

Answer 1

Ratio of area of the square to the area of the circle = π/4

Explanation:

Let the side of square be a and radius of circle be r.

The perimeter of a particular square and the circumference of a particular circle are equal.

Perimeter of square = 4 x a = 4a

Circumference of circle = 2πr

Given that

4a = 2πr

`a=(\pi r)/(2)`

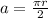
We need to find the ratio of the area of the square to the area of the circle.

Area of the square = a²

Area of the circle = πr²

`\texttt{Ratio of area of the square to the area of the circle =}(a^2)/(\pi r^2)\\\\\texttt{Ratio of area of the square to the area of the circle =}(\left ( (\pi r)/(2)\right )^2)/(\pi r^2)\\\\\texttt{Ratio of area of the square to the area of the circle = }(\pi)/(4)`

Ratio of area of the square to the area of the circle = π/4