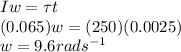Question

A 780g, 50-cm-long metal rod is free to rotate about a frictionless axle at one end. While at rest, the rod is given a short but sharp 1000N hammer blow at the CENTER of the rod, aimed in a direction that causes the rod to rotate on the axle. The blow lasts a mere 2.5ms.

What is the rod's angular velocity immediately after the blow? The book gives the answer 8.0rad/s

Answer 1

9.6 rad/s

Step-by-step explanation:

`L` = length of the metal rod = 50 cm = 0.50 m

`M` = Mass of the long metal rod = 780 g = 0.780 kg

Moment of inertia of the rod about one end is given as

`I = (ML^(2))/(3) = ((0.780)(0.50)^(2))/(3) = 0.065 kgm^(2)`

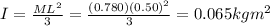
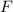`F` = force applied by the hammer blow = 1000 N

Torque produced due to the hammer blow is given as

`\tau = (FL)/(2)`

`\tau = ((1000)(0.50))/(2)`

`\tau = 250 Nm`

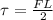
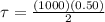
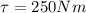
`t` = time of blow = 2.5 ms = 0.0025 s

`w` = Angular velocity after the blow

Using Impulse-change in angular momentum, we have

`I w = \tau t\\(0.065) w = (250) (0.0025)\\w = 9.6 rads^(-1)`