Question

A 98-kg fullback, running at 5.0 m/s, attempts to dive directly across the goal line for a touchdown. Just as he reaches the line, he is met head-on in midair by two 68-kg linebackers both moving in the direction opposite the fullback. One is moving at 2.0 m/s, the other at 4.0 m/s. They all become entangled as one mass.

(a) Sketch the event, identifying "before" and "after" situations. (Do this on paper. Your instructor may ask you to turn in this work.) This answer has not been graded yet.
(b) What is the velocity of the football players after the collision? (Take the positive direction to be the initial direction of the fullback.) m/s
(c) Does the fullback score a touchdown?
Yes
No

Answer 1

(a) Explained below

(b)
`v_f=0.35\ m/s`

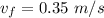
(c) Yes

Step-by-step explanation:

Law Of Conservation Of Linear Momentum

The total linear momentum of a system of particles or objects is conserved unless an external force is acting on the system. The formula for the momentum of a body with mass m and velocity v is P=mv. If there is a system of bodies, then the total linear momentum is the sum of the individual momentums

`P=m_1v_1+m_2v_2+...+m_nv_n`

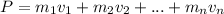
When objects collide and join together, the only final mass is the sum of all masses, all traveling at the same speed.

Our
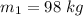`m_1=98\ kg` fullback runs at
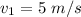`v_1=5\ m/s`. Two two 68-kg linebackers attempt to stop him, one at -2.0 m/s and the other at -4.0 m/s. The negative value is because the run against the positive direction, taken in the direction of the fullback.

(a) Before the event, there is a total linear momentum, computed as the sum of the momentums of each player as shown

`p_1=m_1v_1=(98)(5)=490 Kg\ m/s`

`p_2=m_2v_2=(68)(-4)=-272 kg\ m/s`

`p_3=m_3v_3=(68)(-2)=-136 kg\ m/s`

`p_t=p_1+p_2+p_3=390-272-136=82\ kg\ m/s`

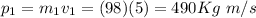
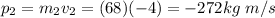
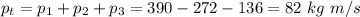
After the collision, all the players keep joined in one single mass of.

`m_t=98+68+68=234\ kg`

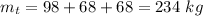
They will move at a speed which will be computed below

(b) The final momentum of the system is

`p_f=m_tv_f=82\ kg\ m/s`

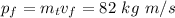
Since the linear momentum is conserved, the final speed
`v_f` is common to all of the players. Let's solve to find it

`\displaystyle v_f=(p_f)/(m_t)`

`\displaystyle v_f=(82)/(234)`

`v_f=0.35\ m/s`

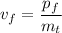
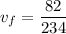
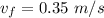
(c) Since the final speed of the players is positive, it means the touchdown was actually scored, the fullback moved forward across the goal line, the positive reference.