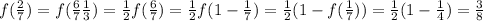Question

The function $f(x),$ defined for $0 \le x \le 1,$ has the following properties:________

(i) $f(0) = 0.$
(ii) If $0 \le x < y \le 1,$ then $f(x) \le f(y).$
(iii) $f(1 - x) = 1 - f(x)$ for all $0 \le x \le 1.$
(iv) $f \left( \frac{x}{3} \right) = \frac{f(x)}{2}$ for $0 \le x \le 1.$ Find $f \left( \frac{2}{7} \right).$

Answer 1

`f((2)/(7)})=(3)/(8)`

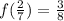
Explanation:

By properties i) and iii),
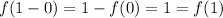`f(1-0)=1-f(0)=1=f(1)`. Now we can use properties iii) iv) to compute some values of f. Namely:

`f((1)/(2))=f(1-(1)/(2))=1-f((1)/(2)) \rightarrow f((1)/(2))=(1)/(2)`

`f((1)/(3))=(f(1))/(2)=(1)/(2)`

`f((1)/(6))=f((1)/(2) (1)/(3))=(f((1)/(2)))/(2)=(1)/(2)(1)/(2)=(1)/(4)`

`f((1)/(9))=f((1)/(3) (1)/(3))=(f((1)/(3)))/(2)=(1)/(2)(1)/(2)=(1)/(4)`

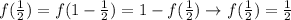
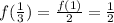
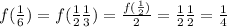
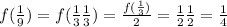
With these values, we can obtain f(1/7) using property ii). Note that:

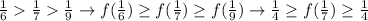`(1)/(6)>(1)/(7)>(1)/(9) \rightarrow f((1)/(6))\geq f((1)/(7))\geq f((1)/(9)) \rightarrow (1)/(4) \geq f((1)/(7)) \geq (1)/(4)` then
`f((1)/(7)})=(1)/(4)`.

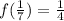Finally, combine the previous work with properties iii) and iv) to get

`f((2)/(7))=f((6)/(7) (1)/(3))=(1)/(2)f((6)/(7))=(1)/(2) f(1-(1)/(7))=(1)/(2)(1-f((1)/(7)))=(1)/(2) (1-(1)/(4))=(3)/(8)`