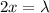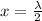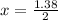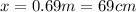Answer:
a. constructive interference takes place.
b. x = 0.34 m= 34 cm
c..
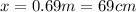
Step-by-step explanation:
Given
Distance between speakers = 12.0 m
frequency = 245 Hz,
speed of sound = 340 m/s,
a. For constructive interference we have
the path difference is

where m = +/-1,+/-2,+/-3,..........
Wavelength of sound =
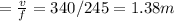
As women is at center or middle point, therefore the path difference at that point must be zero
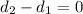
Now the path difference
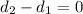 is an integral multiple of the wavlenght therefore constructive interference takes place.
is an integral multiple of the wavlenght therefore constructive interference takes place.
b.
for the sound to reach a minimum intensity
Now if she moves x distance from current point then
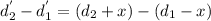
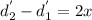
for hearing minimum intensity the interference must be destructive therefore,
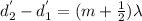
for m = 0

by putting the value of lamda = 1.38 and difference in distance as 2x
we get
x = 0.34 m= 34 cm
c.
for the sound to reach a maximum intensity
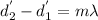
for that m=1