Question

Two airplanes are approaching the airport tower at the same altitude. Radar shows that plane A is 20 miles due east of the tower and that plane B is 22 miles at 15° north of east. (See the drawing provided above).

How far apart are the two planes? Round to the nearest hundredths.


Answer: ___ miles

Answer 1

40 miles

Explanation:

We can solve this by drawing a triangle if one plane is east of the tower and the other north east. We assume that the tower is the other point of the triangle. We have an angle of 15 degrees connecting tower to plan B. We can sine rule to solve this problem.

The sine rule is:

sinA/a=sinB/b=sinC/c

As we know one angle and two sides we can solve for the one side and two angles as we have 3 unknowns and 3 known values:

Let plane A have angle A and side a, plane B have angle B and side b:

sinA/a=sinB/b

sinA/20=sin15/22

sinA
`=(0.259/22)\cdot{20}=0.235`

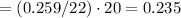
A = sin^-1 (0.235)=13.6 degrees

Therefore angle C is:

`180-13.6-15=151.4`

We can solve for c:

sinB/b=sinC/c

`0.259/22=0.479/c`

`c=40.6`

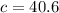
The planes are 40.6 miles apart