Question

Two different simple random samples are drawn from two different populations. The first sample consists of 30 people with 16 having a common attribute. The second sample consists of 1900 people with 1337 of them having the same common attribute. Compare the results from a hypothesis test of p 1 equals 2 ​(with a 0.01 significance​ level) and a 99​% confidence interval estimate of p 1 minus 2.

Answer 1

• There is no significant evidence that p1 is different than p2 at 0.01 significance level.

• 99% confidence interval for p1-p2 is -0.171 ±0.237 that is (−0.408, 0.066)

Explanation:

Let p1 be the proportion of the common attribute in population1

And p2 be the proportion of the same common attribute in population2

`H_(0)`: p1-p2=0

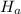`H_(a)`: p1-p2≠0

Test statistic can be found using the equation:

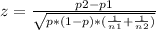`z=\frac{p2-p1}{\sqrt{{p*(1-p)*((1)/(n1) +(1)/(n2)) }}}` where

• p1 is the sample proportion of the common attribute in population1 (
  `(16)/(30) =0.533`)

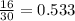• p2 is the sample proportion of the common attribute in population2 (
  `(1337)/(1900) =0.704`)

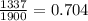• p is the pool proportion of p1 and p2 (
  `(16+1337)/(30+1900)=0.701`)

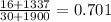• n1 is the sample size of the people from population1 (30)

• n2 is the sample size of the people from population2 (1900)

Then
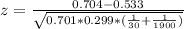`z=\frac{0.704-0.533}{\sqrt{{0.701*0.299*((1)/(30) +(1)/(1900)) }}}` ≈ 2.03

p-value of the test statistic is 0.042>0.01, therefore we fail to reject the null hypothesis. There is no significant evidence that p1 is different than p2.

99% confidence interval estimate for p1-p2 can be calculated using the equation

p1-p2±
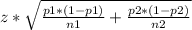`z*\sqrt{(p1*(1-p1))/(n1)+(p2*(1-p2))/(n2)}` where

• z is the z-statistic for the 99% confidence (2.58)

Thus 99% confidence interval is

0.533-0.704±
`2.58*\sqrt{(0.533*0.467)/(30)+(0.704*0.296)/(1900)}` ≈ -0.171 ±0.237 that is (−0.408, 0.066)