Answer:
1.0000
Explanation:
Given that a door delivery florist wishes to estimate the proportion of people in his city that will purchase his flowers.
True proportion = 0.05
sample size n = 355
Sample proportion mean= 0.05
Sample proportion std error =
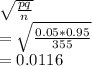
Probability that the sample proportion will differ from the population proportion by more than 0.03
=
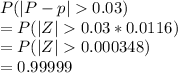
i.e. almost certain