Question

What attributes of the representative model of the parabola can be determined from the standard form

Answer 1

Vertex (h,k)

X intercepts and Y intercepts

Focus

Axis of symmetry

Maximum or minimum value

Explanation:

The general form for a parabola or a quadratic function is given by:

`f(x) = ax^2 +bx+c`

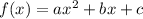
Where a,b and c are real numbers with
`a \\eq 0`.

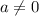Some features that we can identify from the standard form are:

If
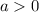`a>0` the parabola opena upward.

If
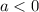`a<0` the parabola open downwards.

We can find the axis of symmetry . And is defined as
`x = - (b)/(2a)`

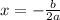
The x intercepts are given by:

`x =(-b \pm √(b^2 -4ac))/(2a)`

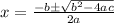
We can find the x intercept with the following formula:

`x = -(b)/(2a)`

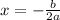
And for the y intercept we just need to use x=0 and we got
`y=c`

And for the y intercept we just need to replace the x intercept into the equation like this:

`y = a( -(b)/(2a))^2 + b( -(b)/(2a))+c`

From the standard from we can also find the domain and range. The minimum or maximum value. And we can also find the focus.