Question

Let f be the function defined as follows:

(attached)


If a = 2 and b = 3, is f continuous at x = 1? Justify your answer.

Find a relationship between a and b for which f is continuous at x = 1.
Hint: A relationship between a and b just means an equation in a and b.

Find a relationship between a and b so that f is continuous at x = 2.

Use your equations from parts (ii) and (iii) to find the values of a and b so that f is continuous at both x = 1 and also at x = 2?

Graph the piece function using the values of a and b that you have found. You may graph by hand or use your calculator to graph and copy and paste into the document.

Answer 1

a = -2; b = 4

Explanation:

I graphed your piecewise function in Figure 1.

The relation involving a and b is a parabola. It is the green segment in the middle of the graph. We must find values of a and b that make the parabola connect with the ends of the straight lines.

We could make the function continuous if the vertex were at (1, 2) and the x-intercept were at (2, 0).

The vertex form of the equation for a parabola is

y = a(x - h)² + k

where h and k are the coordinates of the vertex and a is a constant.

Data:

Vertex at (1, 2)

x-intercept at (2, 0)

Calculations:

1. Substitute the coordinates of the vertex into the equation

y = a(x - 1)² + 2

2. Substitute the coordinates of the x-intercept into the equation and solve for a

`\begin{array}{rcl}0&=& a(2 - 1)^(2) + 2\\0& = & a + 2\\a& = & -2\\\\\end{array}\\`

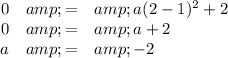
Thus, in the vertex form, a = -2, h = 1, k = 2

3. Determine the equation of the parabola in standard form

y = a(x - h)² + k = -2(x - 1)² + k = -2(x²- 2x + 1) + 2 = -2x² + 4x - 2 + 2

= -2x² + 4x

The values of a and b in the missing segment are -2 and + 4.

I graphed the missing parabola in Fig.2. It makes your piecewise function continuous.