Question

A sample of 300 urban adult residents of a particular state revealed 63 who favored increasing the highway speed limit from 55 to 65 mph whereas a sample of 180 rural residents yielded 75 who favored the increase. Does this data indicate that the sentiment for increasing the speed limit is different for the two groups of residents? Conduct a test by using both the critical region method and the p-value method using (alpha) = 0.05.

Answer 1

`z=\frac{0.21-0.417}{\sqrt{0.2875(1-0.2875)((1)/(300)+(1)/(180))}}=-4.85`

`p_v =2*P(Z<-4.85)=1.24x10^(-6)`

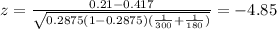
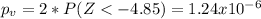
Comparing the p value with the significance level given
`\alpha=0.05` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can conclude that the true proportions are significantly different.

Using the critical method we need to find a value on the normal distribution that accumulates 0.025 of the area on each tail. And for this case we got:

`z_(crit)=\pm 1.96`

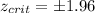
And our rejection zone would be
`(-\infty, -1.96) U(1.96, \infty)`

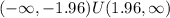
Since our calculated value is on the rejection zone we have enough evidence to reject the null hypothesis at 5% of significance.

Explanation:

1) Data given and notation

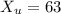`X_(u)=63` represent the number of urban people who favored increasing the highway speed limit from 55 to 65 mph

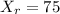`X_(r)=75` represent the number rural of people who favored the increase

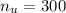`n_(u)=300` sample urban

`n_(r)=180` sample rural

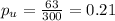`p_(u)=(63)/(300)=0.21` represent the proportion of urban people who favored increasing the highway speed limit from 55 to 65 mph

`p_(r)=(75)/(180)=0.417` represent the proportion of rural people who favored the increase

z would represent the statistic (variable of interest)

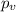`p_v` represent the value for the test (variable of interest)

`\alpha=0.05` significance level given

2) Concepts and formulas to use

We need to conduct a hypothesis in order to check if is there is a difference between the two proportions, the system of hypothesis would be:

Null hypothesis:
`p_(u) - p_(r)=0`

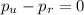
Alternative hypothesis:
`p_(u) - \mu_(r) \\eq 0`

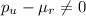
We need to apply a z test to compare proportions, and the statistic is given by:

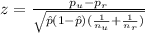`z=\frac{p_(u)-p_(r)}{\sqrt{\hat p (1-\hat p)((1)/(n_(u))+(1)/(n_(r)))}}` (1)

Where
`\hat p=(X_(u)+X_(r))/(n_(u)+n_(r))=(63+75)/(300+180)=0.2875`

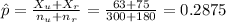
3) Calculate the statistic

Replacing in formula (1) the values obtained we got this:

`z=\frac{0.21-0.417}{\sqrt{0.2875(1-0.2875)((1)/(300)+(1)/(180))}}=-4.85`

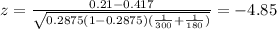
4) Statistical decision

Since is a two side test the p value would be:

`p_v =2*P(Z<-4.85)=1.24x10^(-6)`

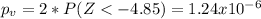
Comparing the p value with the significance level given
`\alpha=0.05` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can conclude that the true proportions are significantly different.

Using the critical method we need to find a value on the normal distribution that accumulates 0.025 of the area on each tail. And for this case we got:

`z_(crit)=\pm 1.96`

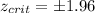
And our rejection zone would be
`(-\infty, -1.96) U(1.96, \infty)`

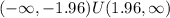
Since our calculated value is on the rejection zone we have enough evidence to reject the null hypothesis at 5% of significance.