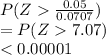Answer:
answer is almost 0 i.e impossible event.
Explanation:
given that the the true population proportion were
p= 0.5
a) Std deviation of sample proportion =

This is the std deviation for a single trial. We know in binomial variance is npq. Using this we can say for a single trial, variance would be pq/n and hence std deviation of proportion is square root of pq/n
b) The probability that the sample proportion will be larger than 0.55 for a random sample ofsize 50
= P(p>0.55)
=