Step-by-step explanation:
Mass of two soccer balls,
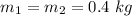
Initial speed of first ball,

Initial speed of second ball,
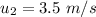
After the collision,
Final speed of the second ball,
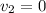
(a) The momentum remains conserved. Using the conservation of momentum to find it as :
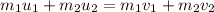
 is the final speed of the first ball
is the final speed of the first ball

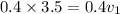
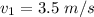
(b) Let
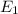 is the kinetic energy of the first ball before the collision. It is given by :
is the kinetic energy of the first ball before the collision. It is given by :
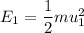

It is at rest, so, the kinetic energy of the first ball before the collision is 0.
(c) After the collision, the second ball comes to rest. So, the kinetic energy of the second ball after the collision is 0.
Hence, this is the required solution.