Question

Bird bones have air pockets in them to reduce their weight—this also gives them an average density significantly less than that of the bones of other animals.

Suppose an ornithologist weighs a bird bone in air and in water and finds its mass is 45.0 g and its apparent mass when submerged is 3.60 g (the bone is watertight).

(a) What mass of water is displaced?

(b) What is the volume of the bone?

(c) What is its average density?

Answer 1

(a). The mass of displaced water is
`41.3*10^(-3)\ kg`

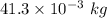
(b). The volume of the bone is
`41.3*10^(-6)\ m^3`

(c). The average density is 1089.58 kg/m³.

Step-by-step explanation:

Given that,

Mass of bone in air = 45.0 g

Mass of bone in water = 3.60 g

(a). We need to calculate the mass of displaced water

Using buoyant force

The buoyant force equal to the difference in apparent weight in air and water

`F_(b)=m_(dw)g`

`m_(dw)g=m_(a)g-m_(w)g`

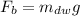
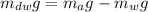
Put the value into the formula

`m_(dw)g=45*10^(-3)*9.8-3.60*10^(-3)*9.8`

`m_(dw)g=0.405`

`m_(dw)=(0.405)/(9.8)`

`m_(dw)=0.0413\ kg`

`m_(dw)=41.3*10^(-3)\ kg`

`m_(dw)=41.3\ g`

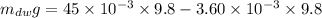
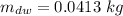
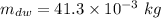
(b). We need to calculate the volume of the bone

Using formula of volume

`V_(dw)=(m_(dw))/(\rho_(w))`

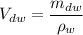
We know that,

`V_(dw)=V_(b)`

Put the value into the formula

`V_(dw)=(41.3*10^(-3))/(1000)`

`V_(dw)=41.3*10^(-6)\ m^3`

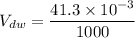
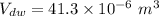
(c). We need to calculate the average density

Using formula of density

`\rho_(b)=(m_(a))/(V_(b))`

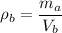
Put the value into the formula

`\rho_(b)=(45.0*10^(-3))/(41.3*10^(-6))`

`\rho_(b)=1089.58\ kg/m^3`

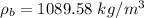
Hence, (a). The mass of displaced water is
`41.3*10^(-3)\ kg`

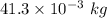
(b). The volume of the bone is
`41.3*10^(-6)\ m^3`

(c). The average density is 1089.58 kg/m³.