Question

A 3-phase induction motor with 4 poles is connected to a voltage source with an amplitude of 209 Vrms and a frequency of 120 Hz. The circuit has negligible line impedance and you can assume the simplified circuit model is valid. The motor has Rs = 2.3 LaTeX: \OmegaΩ, R'r = 0.7 LaTeX: \OmegaΩ, Xs = 1.3 LaTeX: \OmegaΩ, X'r = 1.8 LaTeX: \OmegaΩ , and Xm = 76 LaTeX: \OmegaΩ. In addition, the motor is spinning at a speed of 2,464 rpm. What is the output torque at the specified speed in Nm?

Answer 1

T = 25.41 Nm

Step-by-step explanation:

Calculating Nsync (Synchronous Speed):

`Nsync = 120f/P`

`Nsync = 120 x 120 / 4\\Nsync = 3600 rpm`

`Wsync = 3600 * 2\pi /180\\Wsync = 377 rad/s`

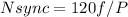
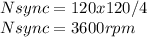
Calculating s (Slip):

`s = (Nsync - Nm) / Nsync \\</p><p>[tex]s = (3600-2464)/3600\\s = 0.3156`

Calculating Vth (Thevenin Voltage):

`Vth = Vph (Xm / \sqrt{Rs^(2) + (Xs+Xm)^(2)  })\\Vth = 209 (76 / \sqrt{(2.3)^(2) + (1.3 + 76)^(2)  }\\Vth = 205.39 V`

Calculating Rth (Thevenin Resistance):

`Rth = Rs (Xm/Xs + Xm)^(2) \\Rth = 2.3 (76/1.3 + 76)^(2) \\Rth = 2.22 ohm`

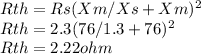
Calculating Xth (Thevenin Reactance):

Xth = Xs = 1.3 ohm

Calculating Torque:

`T = (3Vth^(2)Rr/s) / (Wsync[(Rth+Rr/s)^(2) + (Xth + Xr)^(2)])\\T = (3*205.39*0.7/0.3156) / 377[(2.22+0.7/0.315)^(2) + (1.3+1.8)^(2)]`

T = 280699 / 377 [19.69 + 9.61]

T = 25.41 Nm