1 Answer

Daniel Rafael Wosch · Answer 1 · 2020-05-31T18:25:16+0000

Answer:
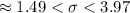
$\approx1.49<\sigma<3.97$

Explanation:

We know that the confidence interval for population standard deviation is given by :-

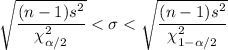
$\sqrt{((n-1)s^2)/(\chi^2_(\alpha/2))}<\sigma<\sqrt{((n-1)s^2)/(\chi^2_(1-\alpha/2))}$

, where n= sample size

s = sample standard deviation.

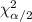$\chi^2_(\alpha/2)$ and
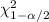$\chi^2_(1-\alpha/2)$ = Chi-square critical value for degree of freedom (n-1) and significance level (
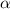$\alpha$ ).

Given :
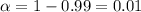
$\alpha=1-0.99=0.01$

n= 16

Critical ch-square values for degree of freedom 15 and
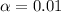$\alpha=0.01$ will be :

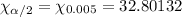
$\chi_(\alpha/2)=\chi_(0.005)=32.80132$

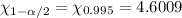
$\chi_(1-\alpha/2)=\chi_(0.995)=4.6009$

Then , the required 99% confidence interval for the population standard deviation will be :

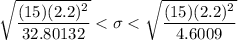
$\sqrt{((15)(2.2)^2)/(32.80132)}<\sigma<\sqrt{((15)(2.2)^2)/(4.6009)}$

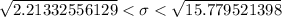
$√(2.21332556129)<\sigma<√(15.779521398)$

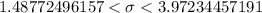
$1.48772496157<\sigma<3.97234457191$

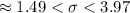
$\approx1.49<\sigma<3.97$

Hence, the a 99% confidence interval for the population standard deviation :

Please log in or register to add a comment.