Question

If they want a sample committee consisting of four male and four female students, from a possible volunteer pool of eight male and seven female students, how many ways can this committee be formed?

Answer 1

There are 2450 ways.

Explanation:

We can pick first the 4 man, and then the 4 women. The configuration of men and women are independant with each other, so the total of possibilities is obtained by multiplying the total possibilities to pick 4 men and the total possibilities of picking 4 women.

To pick 4 men from a group of 8, the total number of possibilities is the amount of ways to pick 4 elements from a group of 8. This number is represented by the combinatorial number of 8 with 4

`{8 \choose 4} = (8!)/(4!4!) = 70`

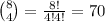
To pick 4 women from a group of 7, we need to count the total amount of ways to pick 4 elements from a group of 7. This is the combinatorial number of 8 with 7

`{7 \choose 4} = (7!)/(4!3!) = 35`

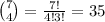
Hence, the total amount of ways to pick 4 men and 4 women from a group of 8 men and 7 women is 70*35 = 2450.