Question

Aluminum wire 1.00 mm in radius is to be used to construct a solenoid 15.0 mm in radius so that the magnitude of the magnetic field at its center is 50.0 mT and the total resistance of the solenoid is 3.00 Ω when it carries a current of 1.00 A. How long does this solenoid need to be? The resistivity of aluminum is 2.655 x 10-8 ohm m.

Answer 1

To solve this problem we will proceed to use the equations given for the calculation of the resistance, in order to find the radius of the cable. Once the length is found we can find the number of turns of the solenoid and finally the net length of it

The resistance of the wire is

`R= (\rho L)/(A)`

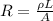
`\rho`= Resistivity

L = Length

A = Cross-sectional Area

That can be also expressed as,

`R = (\rho L)/(\pi r^2)`

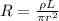
Rearranging the equation for the length of the wire we have

`L= (R\pi r^2)/(\rho)`

`L= (3\Omega \pi(1*10^(-3)))/(2.655*10^(-8)\Omega \cdot m)`

`L = 354.8m`

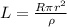
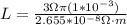
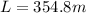
The number of turns of the solenoid is

`N = (L)/(2\pi r) \rightarrow` Denominator is equal to the circumference of the loop

`N = (354.8)/(2\pi(15*10^(-3)))`

`N = 3766`

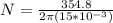
Finally the Length of he solenoid is

`l = N (\phi)`

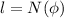
Where \phi is the diameter of wire

`l = N (2r)`

`l = (3766)(2*(1*10^(-3)))`

`l = 7.532m`

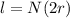
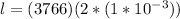
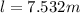
Therefore the length of the solenoid is 7.532m