Answer:
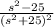
Explanation:
Let's use the definition of the Laplace transform and the identity given:
![\mathcal{L}[t \cos 5t]=(-1)F'(s)](https://img.qammunity.org/2020/formulas/mathematics/college/ejjkbqrkavm59pa8e8jbveh07bzkzk8l34.png) with
with
![F(s)=\mathcal{L}[\cos 5t]](https://img.qammunity.org/2020/formulas/mathematics/college/lb3q1x1gnefsgbop2bisvpdmlhoo5o62uo.png) .
.
Now,
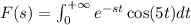 . Using integration by parts with u=e^(-st) and dv=cos(5t), we obtain that
. Using integration by parts with u=e^(-st) and dv=cos(5t), we obtain that
 .
.
Using integration by parts again with u=e^(-st) and dv=sin(5t), we obtain that
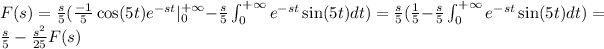 .
.
Solving for F(s) on the last equation,
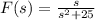 , then the Laplace transform we were searching is
, then the Laplace transform we were searching is
