Question

The primary of a step-down transformer has 240 turns and is connected to a 120 V rms line. The secondary is to supply 26 A at 6 V.

(a) Find the current in the primary.
_________A

(b) Find the number of turns in the secondary, assuming 100% efficiency.
_________

A 8 µF capacitor is charged to 33 V and is then connected across a 11-mH inductor.

(a) How much energy is stored in the system?
_________J

(b) What is the frequency of oscillation of the circuit?
________Hz

(c) What is the maximum current in the circuit?
_________A

Answer 1

Step-by-step explanation:

Np = 240

Vp = 120 V

Is = 26 A

Vs = 6 V

(a) According to the principle of transformer

Ip/ Is = Vs / Vp

Ip / 26 = 6 / 120

Ip = 1.3 A

(b) Ns / Np = Vs / Vp

Ns / 240 = 6 / 120

Ns = 12

....................................

C = 8 x 10^-6 F

V = 33 V

L = 11 m H = 0.011 H

(a) Energy stored, U = 0.5 x CV² = 0.5 x 8 x 10^-6 x 33 x 33

U = 4.356 x 10^-3 J

(b) Let f be the frequency of oscillations

`f=(1)/(2\pi √(LC))`

`f=\frac{1}{2* 3.14 \sqrt{0.011* 8*10^(-6)}}`

f = 536.78 Hz

Answer 2

Step-by-step explanation:

Solution (1)

It is given that,

Number of turns in primary coil in step down transformer,
`N_P=240`

Voltage in primary transformer,
`V_p=120\ V`

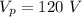
Current in secondary coil,
`I_s=26\ A`

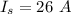
Voltage in secondary coil,
`V_s=6\ A`

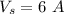
(a) Let
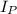`I_P` is the current in primary coil. It can be calculated using the formula as :

`(V_P)/(V_s)=(I_s)/(I_P)`

`(120)/(6)=(26)/(I_P)`

`I_p=1.3\ A`

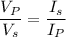
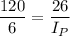
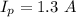
(b) Let
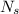`N_s` is the number of turns in secondary coil. It can be calculated using the formula as :

`(V_P)/(V_s)=(N_P)/(N_s)`

`(120)/(6)=(240)/(N_s)`

`N_s=12\ turns`

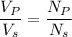
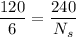
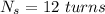
Solution (2)

Capacitance of the capacitor,
`C=8\ \mu F=8* 10^(-6)\ F`

Voltage, V = 33 V

Inductance,
`L=11\ mH=11* 10^(-3)\ H`

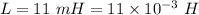
(a) Let E is the energy stored in the system. It is given by :

`E=(1)/(2)CV^2`

`E=(1)/(2)* 8* 10^(-6)* (33)^2`

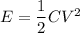
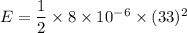
E = 0.00435 J

or

`E=4.35* 10^(-3)\ J`

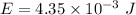
(b) Let f is the frequency of oscillation. It is given by :

`f=(1)/(2\pi √(LC) )`

`f=\frac{1}{2\pi \sqrt{11* 10^(-3)* 8* 10^(-6)} }`

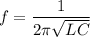
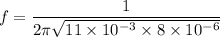
f = 536.51 Hz

(c) The maximum current in the circuit is,

`I=\sqrt{(2E)/(L)}`

`I=\sqrt{(2* 0.00435)/(11* 10^(-3))}`

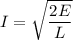
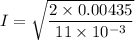
I = 0.88 A

Hence, this is the required solution.