Question

Two crates of mass 65 kg and 125 kg ,are in contact and at rest ona horizontal surface. a 650 N force is exerted on the 65 kg crate.if the coefficient of kinetic friction is 0.18 calculatea) the acceleration of the system andb)the force that each crate exerts on the other.c) repeat with the crates reversed

Answer 1

Step-by-step explanation:

m = 65 kg

M = 125 kg

F = 650 N

μ = 0.18

(a) Let a be the acceleration of the system

Let f be the force of contact between the two.

use newton's second law

F - f - μmg = m x a .... (1)

f - μMg = M x a... (2)

Add both the equations

F - μ(M + m) g = (M + m) a

650 - 0.18 (65 + 125) x 9.8 = (65 + 125) a

a = 1.657 m/s²

(b) Put the value in equation (2)

f - 0.18 x 125 x 9.8 = 125 x 1.657

f = 207.125 + 220.5

f = 427.625 N

(c) if the crates are reversed, the acceleration remains same.

f - 0.18 x 65 x 9.8 = 65 x 1.657

f - 114.66 = 107.705

f = 222.365 N

Answer 2

(a). The acceleration of the system is 1.65 m/s².

(b). The force that each crate exerts on the other is 426.75 N.

(c). The force that each crate exerts on the other when the crates reversed is 221.91 N.

Step-by-step explanation:

Given that,

Mass of first crates = 65 kg

Mass of second crates = 125 kg

Force = 650 N

Coefficient of kinetic friction = 0.18

(a). We need to calculate the acceleration of the system

Using balance equation

`(m_(1)+m_(2))a=F-F_(fr)`

`(m_(1)+m_(2))a=F-\mu(m_(1)+m_(2))g`

`a=(F)/((m_(1)+m_(2)))-\mu g`

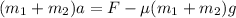
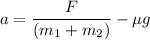
Put the value into the formula

`a=(650)/(65+125)-0.18*9.8`

`a=1.65\ m/s^2`

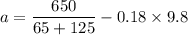
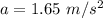
(b). We need to calculate the force that each crate exerts on the other

Using balance equation

`F-F_(fr)=m_(2)a`

`F=m_(2)a+\mu m_(2)g`

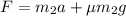
Put the value into the formula

`F=125*1.65+0.18*125*9.8`

`F=426.75\ N`

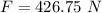
(c). If the crates reversed,

We need to calculate the force that each crate exerts on the other

Using balance equation

`F-F_(fr)=m_(2)a`

`F=m_(2)a+\mu m_(2)g`

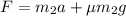
Put the value into the formula

`F=65*1.65+0.18*65*9.8`

`F=221.91\ N`

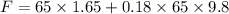
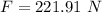
Hence, (a). The acceleration of the system is 1.65 m/s².

(b). The force that each crate exerts on the other is 426.75 N.

(c). The force that each crate exerts on the other when the crates reversed is 221.91 N.